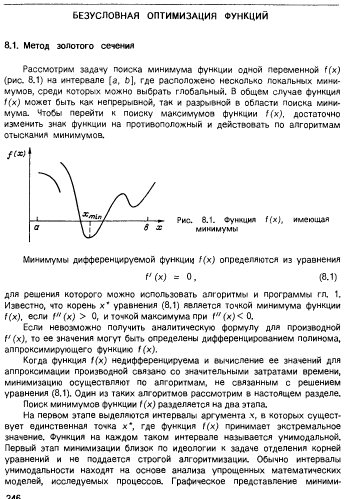
5.7. Методы золотого сечения и Фибоначчи.

Эти методы основываются на одном и том же алгоритме перехода к следующей пробной точке и отличаются лишь способом выбора первой точки. В результате каждого шага (добавления одной пробной точки) мы получаем отрезок Lⁿ = [aⁿ, bⁿ] с одной "старой" пробной точкой xⁿ ∈ (aⁿ, bⁿ). "Новая" пробная точка yⁿ определяется как точка симметричная xⁿ относительно центра отрезка Lⁿ:

yn =  an + bn 2  +  ( an + bn 2  – xn )  = an + bn – xn

Затем, в зависимости от того, какое из неравенств f(xⁿ) ≤ f(yⁿ) или f(xⁿ) > f(yⁿ) выполняется, в качестве Lⁿ⁺¹ выбирается или отрезок [aⁿ, yⁿ], или [xⁿ, bⁿ] (здесь мы считаем для определенности, что xⁿ < yⁿ), а в качестве старой пробной точки xⁿ⁺¹ выбирается либо xⁿ, либо yⁿ.

З а д а ч а  5.10*. Докажите, что l^n–1 = lⁿ + lⁿ⁺¹, где lⁿ — длина отрезка Lⁿ.

В методе золотого сечения x⁰ делит отрезок [a, b] по правилу золотого сечения:

b – a x0 – a  = τ,

где τ — положительный корень уравнения

τ2 = τ + 1

(золотое сечение): τ = (1 + √5)/2 ≈ 1.618). Таким образом, l⁰ = l¹τ. Но тогда (см. задачу 5.10) l² = l⁰ – l¹ = l¹(τ– 1) = l₁/τ, т. е. l¹ = l²τ.

З а д а ч а  5.11. Докажите, что lⁿ⁺¹ = lⁿ/τ.

Поэтому после n + 1 эксперимента

ln =  l τn .

В частности, для уменьшения отрезка неопределенности в 10⁶ раз нужно провести 29 вычислений функции (ср. с 40 вычислениями в методе дихотомии).

В методе Фибоначчи сначала задается число n вычислений функции и затем первая пробная точка подбирается таким образом, чтобы последняя пара экспериментов давала отрезок неопределенности наименьшей длины, т. е. чтобы последние две точки составляли симметричную относительно центра отрезка пару, расстояние между которыми равно ε. Таким образом,

ln–1 = 2ln – ε.

Учитывая, что (см. задачу 5.10)

ln–2 = ln–1 + ln,

получаем l^n–2 = 3lⁿ – ε, l^n–3 = 5lⁿ– 2ε, l^n–4 = 8lⁿ – 3ε, l^n–5 = 13lⁿ – 5ε и  т. д. Индукцией по i легко доказывается, что

ln–i = Fi+1ln – Fi–1ε,

(15)

где Fⁱ — так называемые числа Фибоначчи, определяемые соотношениями F⁰ = F¹ = 1, Fⁱ = F^n–1 + F^n–2, i = 2,3, ..., введенные в XIII веке Леонардом Пизанским (Фибоначчи) совсем по другому поводу¹⁾. Из (15) мы получаем, во-первых, длину lⁿ отрезка неопределенности, получающегося в результате вычисления f в n + 1 точках:

l = l0 = Fn+1ln – Fn–1ε,

откуда

ln =  l Fn+1  +  Fn–1 Fn+1 ε,

и, во-вторых, длину отрезка l¹, задающего положение первой (стартовой) точки:

l1 = Fnln – Fn–2ε =  Fn Fn+1 l +  FnFn–1 – Fn–2Fn+1 Fn+1 ε.

(16)

З а д а ч а  5.12. Докажите, что (Fⁱ)² = F^i–1Fⁱ⁺¹ + (–1)ⁱ. Используя это тождество, получите из (16) более простое соотношение, определяющее lⁿ:

ln =  Fn Fn+1 l +  (–1)n Fn+1 ε.

(17)

Таким образом, чтобы запустить метод Фибоначчи необходимо заранее знать количество точек, в которых будет вычисляться функция f. В то же время метод Фибоначчи является наилучшим алгоритмом в таком классе методов²⁾, в частности, по сравнению с методом золотого сечения, за одно и то же число шагов он дает отрезок неопределенности в τ²/√5 ≈ 1.17 раз меньший. На практике чаще используют первый из них, поскольку выигрыш в методе Фибоначчи не велик, а необходимость заранее знать число n вычислений функции зачастую обременительна.

Отметим еще, что описанные методы одномерной оптимизации эффективны в случаях, когда у нас либо не дифференцируема функция, либо вычисление производных дорого стóит. В противном случае чаще используют методы первого или второго порядков.