2.4. Транспортная задача

Важный тип задач линейного программирования представляет задача о перевозках. Называется она так потому, что цель этой задачи заключается в минимизации полной стоимости перевозок известного количества товаров со складов к потребителю.

Сбалансированная задача - задача о перевозках, в которой общий объем товаров, готовых к отправлению, в точности равен объему товаров, который готовы принять в пунктах назначения.

Пример 1. Рассмотрим транспортную задачу, заданную таблицей

Решение. Пусть - искомое число единиц товара, пересылаемого из пункта в пункт . Тогда данные таблицы можно представить в следующем виде:

при условии, что

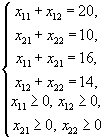
Положим и выразим через t остальные переменные:
из первого уравнения: ,
из второго уравнения: ,
из третьего уравнения:

Тогда

Из того, что все не отрицательны, получаем, что переменная t должна удовлетворять одновременно следующим четырем неравенствам:

Тем самым, мы получили условие .

Не трудно заметить, что при t = 16.

Ответ:

		В			Наличие
		1	2	3
А	1	8	5	6	120
	2	4	9	7	180
Запрос		70	140	90	300

Пример 2. Компания имеет два товарных склада и трех оптовых покупателей. Известно, что общий объем запасов на складах составляет 300 тыс. единиц продукции и совпадает с общим объемом заказов покупателей.

Обозначим через количество товара, поставляемого со склада покупателю .

Тогда соответствующая транспортная задача может быть сформулирована следующим образом.

Минимизировать общую стоимость перевозок:

при условии, что

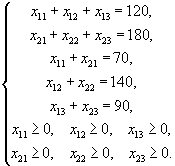
Получаем задачу линейного программирования, в которой основные ограничения вследствие того, что транспортная задача сбалансирована, является равенствами.

Положим и выразим через u и v остальные переменные. Имеем

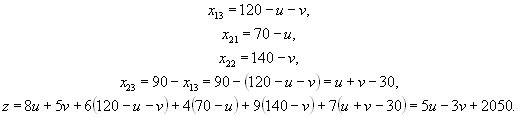
Учитывая, что все перевозки должны получить неотрицательные значения, мы приходим к задаче

которую можно решить графическим методом.

Выписанные неравенства определяют на плоскости (u, v) пятиугольник с вершинами (30, 0), (70, 0), (70, 50), (0, 120), (0, 30).

Ответ: