РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Будем рассматривать дифференциальное уравнение второго порядка.
![]() , (1)
, (1)
где ![]() ,
, ![]() ,
, ![]() −
заданные непрерывные на отрезке [a, b] функции.
−
заданные непрерывные на отрезке [a, b] функции.
Напомним, что задача Коши для уравнения (1) сводится к нахождению
решения ![]() , удовлетворяющего начальным условиям:
, удовлетворяющего начальным условиям:
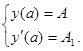
Краевой задачей называется задача нахождения решения ![]() , удовлетворяющего граничным условиям:
, удовлетворяющего граничным условиям:
![]() (2)
(2)
Краевая задача отличается от задачи Коши непредсказуемостью. Ее решение может существовать, не существовать, быть единственным, может быть бесконечно много решений.
Часто вместо граничных условий (2) используют обобщенные граничные условия:
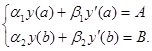 (3)
(3)
Граничные условия называются однородными, если A=B=0.
Соответственно,
краевая задача называется однородной,
если у нее однородные граничные условия и правая часть уравнения ![]() .
.
Следующая теорема имеет важное теоретическое значение.
Теорема. Краевая задача (1) , (3) имеет решение, причем единственное тогда и только тогда, когда соответствующая ей однородная краевая имеет только нулевое решение (тривиальное решение однородной краевой задачи).
Способы решения краевой задачи (хз надо или нет).
Поскольку достаточно хороших аналитических методов нет, то используются приближенные методы.
Система дважды непрерывно дифференцируемых функций ![]() называется базисной системой, если
выполняется:
называется базисной системой, если
выполняется:
1) ![]() удовлетворяет граничному условию (3),
удовлетворяет граничному условию (3),
2) функции ![]() − линейно независимы на [a, b] и удовлетворяют однородным граничным условиям.
− линейно независимы на [a, b] и удовлетворяют однородным граничным условиям.
По базисным функциям строят приближенное решение:
![]() .
.
Задача сводится к выбору коэффициентов ![]() таких,
чтобы функция
таких,
чтобы функция
yn(x) удовлетворяла граничному условию (3) и была в некотором смысле близкой к точному решению.
Поступают следующим образом. Выражение
![]() называют невязкой.
называют невязкой.
Легко видеть, что, если бы ![]() , то yn(x) было бы
точным решением. К сожалению, так бывает очень редко. Следовательно, необходимо
выбрать коэффициенты таким образом, чтобы невязка была в некотором смысле
минимальной.
, то yn(x) было бы
точным решением. К сожалению, так бывает очень редко. Следовательно, необходимо
выбрать коэффициенты таким образом, чтобы невязка была в некотором смысле
минимальной.
Метод коллокаций.
На отрезке [a, b] выбираются точки![]() , которые
называются точками коллокации. Точки коллокации последовательно подставляются в
невязку. Считая, что невязка должна быть равна нулю в точках коллокации, в
итоге получаем систему уравнений для определения коэффициентов
, которые
называются точками коллокации. Точки коллокации последовательно подставляются в
невязку. Считая, что невязка должна быть равна нулю в точках коллокации, в
итоге получаем систему уравнений для определения коэффициентов ![]() .
.
 (4)
(4)
Обычно m=n. Получается система из n линейных
уравнений с n неизвестными (коэффициентами ![]() ):
):
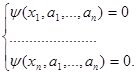
Решая (4), найдем приближенное решение yn(x). Для повышения точности расширяем базисную систему. Получаем более точное решение.
В значительной степени успех в применении метода зависит от удачного выбора базисной системы.
Пример. Пусть
![]() ,
,
![]() ,
, ![]() .
.
Выберем базисную систему:
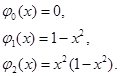
Поскольку ![]() , следовательно, функции
, следовательно, функции ![]() и
и ![]() линейно независимы.
линейно независимы.
Строим приближенное решение
![]() .
.
Выберем точки коллокации:
![]() .
.
Получаем систему уравнений
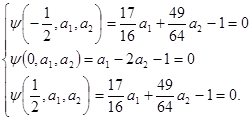
Решая ее, получим
![]() .
.
Метод наименьших квадратов.
Как и в методе коллокаций приближенное решение строится по базисной
системе. Для нахождения коэффициентов при базисных функциях минимизируется
интеграл 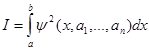 .
.
Строим систему
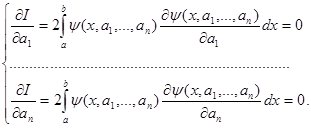
Решая ее, находим ![]() .
.
Синтезом метода наименьших квадратов и метода коллокаций
является следующий метод. Выбирают N>n точек и решают задачу
![]() .
.
Для ее решения строится система
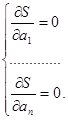
Пример. Рассмотрим краевую задачу
![]()
![]()
Выберем базисную систему:
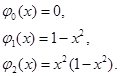
Применяя метод наименьших квадратов, можно найти
![]()
Метод Галеркина.
По базисной системе строим приближенное решение
![]() .
.
Рассматриваем невязку ![]() и для определения
коэффициентов при базисных функциях строим систему
и для определения
коэффициентов при базисных функциях строим систему
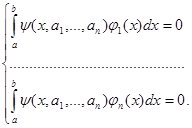
Решая данную систему, находим значение ![]() .
.
Пример. Рассмотрим краевую задачу
![]()
![]() .
.
Возьмем
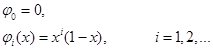
Тогда, применяя метод Галеркина, получим
![]()
![]()
Сравним значения точного решения ![]() со
значениями приближенных решений
со
значениями приближенных решений ![]() и
и ![]() в
отдельных точках.
в
отдельных точках.
|
xi |
|
|
|
|
0,25 0,5 0,75 |
0,044 0,07 0,06 |
0,052 0,069 0,052 |
0,044 0,062 0,06 |
Разностный метод решения краевых задач.
Рассмотрим краевую задачу
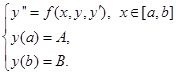 (5)
(5)
Разобьем отрезок [a, b] на n одинаковых частей с шагом ![]() точками:
точками:
![]() .
.
Заменим
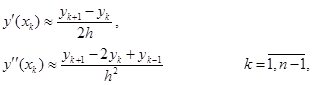
где ![]() .
.
Получаем для любого
внутреннего узла ![]() ,
, ![]() уравнение
уравнение
![]() (6)
(6)
и для граничных узлов
![]() .
.
То есть мы имеем
систему из (n+1)
уравнения с (n+1)
неизвестными ![]() . Ее решение дает нам приближенное решение
краевой задачи.
. Ее решение дает нам приближенное решение
краевой задачи.
Рассмотрим частный случай линейной краевой задачи:
![]() , (7)
, (7)
![]() .
.
В этом случае получаем
![]() (8)
(8)
![]() .
.
То есть получили трехдиагональную систему линейных уравнений
![]() ,
,
в которой выполнено условие преобладания диагональных элементов
![]() .
.
Такая система легко решается методом прогонки.