ВЫБОР МЕТОДА РЕШЕНИЯ СИСТЕМЫ ОДУ ПРИ МОДЕЛИРОВАНИИ РАЗВЕРТЫВАНИЯ ТРОСОВОЙ СИСТЕМЫ КАК СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
С середины 60-х годов появился интерес к использованию тросо- вых систем (ТС) в космосе. Описано множество применений ТС, но прежде чем использовать тросовую систему ее надо сначала привести в рабочее состояние. В работе рассматривается связка из двух объек- тов: спутника и капсулы. В начальный момент времени они объедине- ны в единое целое и развертывание связки представляет собой про- цесс перевода спутника и капсулы в состояние, когда они находятся на некотором расстоянии друг от друга, оставаясь соединенными тро- сом. Механизм отделения сообщает капсуле начальную скорость 2 м/с, направленную по локальной геовертикали к Земле, и разверты- вание происходит под действием гравитационных сил, силы натяже- ния троса и сил аэродинамического сопротивления без использования реактивных двигателей.
Настоящая работа посвящена моделированию и численному ре- шению задачи развертывания ТС. В качестве базовой была взята ма- тематическая модель из [1]. Однако потребовалась ее доработка, по- скольку в данном случае система имеет переменное количество эле- ментов, а также добавляется сила, действующая на первый элемент системы со стороны управляющего механизма [2].
Так же для моделирования развертывания потребовалось реали- зовать несколько методов решения системы ОДУ, поскольку исполь- зуемый в [1] метод Рунге–Кутты–Фехлберга (rkf45) оказался не ус- тойчивым. В качестве альтернативы были реализованы методы Адам- са–Бэшфорта–Мултона (АБМ), Розенберга (W-method, далее ros4w) и метод дифференцирования назад (bdf). Все методы имеют четвертый порядок точности. Также исследовалось влияние длины элементов li системы и соответственно их количества на устойчивость решения.
Моделировалось развертывание тросовой системы в течении 2 700 сек при начальной высоте круговой орбиты 300 км.
Влияние шага. Результаты, для различных методов, длин эле- ментов и величин шага показаны в табл. 1. В большинстве случаев 104 при малом шаге различные методы дают близкий результат, разли- чающийся менее чем на 0,3%. Однако на рис. 1 показана принципи- ально иная ситуация. Графики расходятся и резко отличаются от ре- зультатов других вычислений. Используемые методы становятся не- устойчивыми. Лучше всех себя проявляет метод Адамса–Башфорта– Мултона, а самым неудачным при больших h стал метод диффе- ренцирования назад.
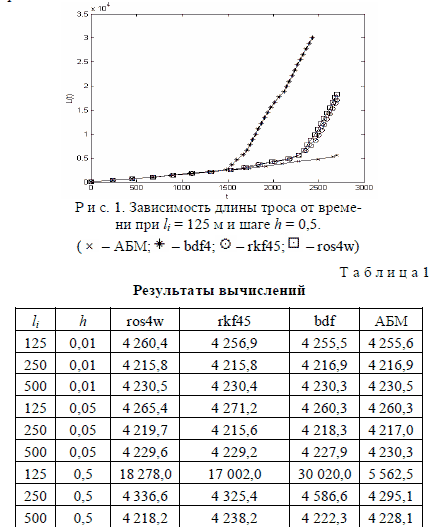
Влияние длины элементов системы. Следует отметить другой фактор, оказывающий существенное влияние на вычислительный процесс – это длина элементов системы. Система уравнений стано- вится более жесткой, вычислительный процесс заметно замедляется. 105 На рис. 2 видно, что с уменьшением длины элемента возрастает неустойчивость, что особенно заметно при li = 125 м. Это видно и из данных табл. 1. Так же в обоих случаях можно заметить похожее влияние уменьшения длины элемента скорость. Компенсировать воз- никающую нестабильность можно уменьшением шага, но это приво- дит к значительному замедлению вычислений (см. табл. 2). При круп- ном шаге более высокую скорость показывают многошаговые методы, а при более мелком быстрее работают одношаговые методы.
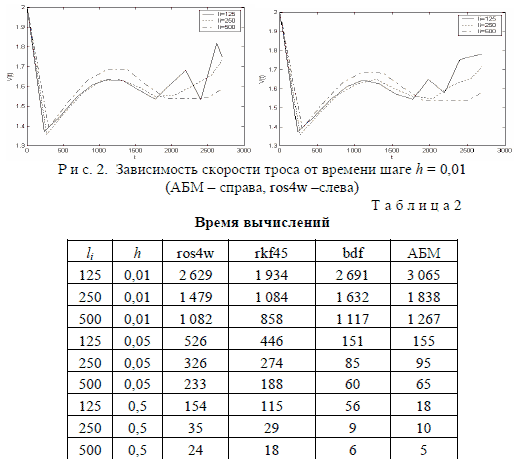
Основываясь на вышесказанном, а также поскольку методы rkf45 и bdf снижают устойчивость при увеличении шага, в качестве самого оптимального был выбран метод Розенброка (модификация Вольф- брандта). На рис. 3 показано изменение шага интегрирования при аб- солютной и относительной ошибке 10–3 и ограничении на шаг 106 0,00001 ≤ h ≤ 0,4, li = 125. Как видно большая часть вычислений про- ходит при h ≈ 0,05. При этом время вычислений составляет 478 сек, что почти на 20% меньше времени, затраченного при моделировании при h = 0,05. При этом полученный результат L = 4 266,7 отличается на 1,3 м, то есть на 0,03%.
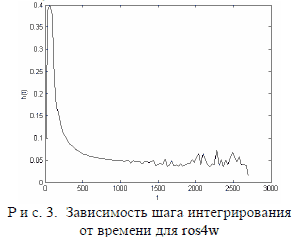
В результате проведенных тестов был выбран метод Розенброка четвертого порядка точности с автоматическим выбором шага. Этот метод, в отличии, например от метода Рунге–Кутты–Фехлберга, по- зволяет преодолевать жесткость системы, которая особенно сильно проявляется при увеличении количества элементов тросовой систе- мы. При этом он показывает более выгодные скоростные качества по сравнению с методом Адамса–Бэшфорта–Мултона.