Краевая задача

          

                                                                                                            ^(8.3)

является нелинейной краевой задачей, если функция  нелинейна хотя бы по одному из аргументов y или

В настоящей работе реализованы два способа решения нелинейных краевых задач: метод стрельбы и метод линеаризации (метод Ньютона), который сводит решение нелинейной краевой задачи к решению серии линейных краевых задач.

 

 

Метод стрельбы

Метод стрельбы для решения краевой задачи (8.3) базируется на том, что имеются удобные способы численного решения задачи Коши, т. е. задачи следующего вида

 

                              (8.4)

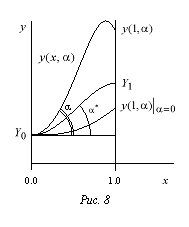
где  — ордината точки  из которой выходит интегральная кривая; a — угол наклона интегральной кривой к оси x при выходе из точки  (рис. 8). При фиксированном  решение задачи (8.4) имеет вид  При  решение  зависит только от a:

Используя указанное замечание о решении задачи Коши (8.4), можно задачу (8.3) переформулировать следующим образом: найти такой угол  при котором интегральная кривая, выходящая из точки  под углом a к оси абсцисс, попадет в точку

                                                                                      (8.5)

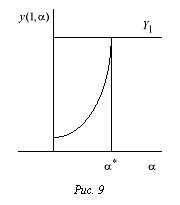
Решение задачи (8.4) при этом  совпадает с искомым решением задачи (8.3). Таким образом, дело сводится к решению уравнения (8.5) (рис. 9). Уравнение (8.5) — это уравнение вида

где

Оно отличается от привычных уравнений лишь тем, что функция  задана не аналитическим выражением, а с помощью алгоритма численного решения задачи (8.4).

Для решения уравнения (8.5) можно использовать любой метод, пригодный для уточнения корней нелинейного уравнения, например, метод деления отрезка пополам, метод Ньютона (касательных) и др. Метод Ньютона здесь предпочтительнее (если имеется достаточно хорошее начальное приближение) из-за высокой стоимости вычисления одного значения функции F(a) (нужно решить задачу Коши (8.4) с данным a).

Метод стрельбы, сводящий решение краевой задачи (8.3) к вычислению решений задачи Коши (8.4), хорошо работает в том случае, если решение  «не слишком сильно» зависит от a. В противном случае он становится вычислительно неустойчивым, даже если решение задачи (8.3) зависит от входных данных «умеренно».

При решении уравнений  методом деления отрезка пополам, мы задаем  и  так, чтобы разности  и  имели разные знаки. Затем полагаем

Вычисляем  Затем вычисляем  по одной из формул:

              или              

в зависимости от того, имеют ли разности  и  соответственно разные или одинаковые знаки. Затем вычисляем  Процесс продолжаем до тех пор, пока не будет достигнута требуемая точность

В случае использования для решения уравнения  метода Ньютона задаем  а затем последующие  вычисляем по рекуррентной формуле

             n = 0, 1, …

Производная  может быть вычислена по одной из формул численного дифференцирования, например, первого порядка аппроксимации: